whoimi

A geek blog

View on GitHub

表面反射模型基础推到

这篇文章主要用来推导、描述表面反射模型：包括PBR的BRDF、BSSRDF、BSDF以及风格化渲染的反射模型、二次元渲染的反射模型等等内容。

光线照射到物体表面，发生反射，之后反射光线进入人眼，最终形成人眼对物体的感觉。

所以最重要的就是光线如何在不同的材质上进行反射，也就是我们现在要研究的反射模型。

BRDF

双向反射分布函数（BRDF）就是最常用的对表面反射的定义。

BRDF描述的问题：当沿着$w_i$方向入射辐射度为时，朝向观察者且方向为的离开当前表面的辐射度。

假设$ w_i $为微分方向视椎体，为入射点，则p处的微分入射辐射度为：

单位辐射角入射光强度

法线和入射角夹角

为微分方向视椎体

我们很容易想到，反射光线和入射光线强度是成正比的：

所以当给定一对如何方向和反射方向，BDRF函数可以写作：

​

上面是BRDF函数，而物理的BRDF函数同时还需要满足：

最终的反射光为：

​

上面的只局限在反射方向，就是法线方向的上半球。

BTDF

而表面还可能有透视光线，即穿透到法线放线下半球的光线，我们用双向透射分布函数表述（BTDF）。和分布于法线两边。

最终的透射光为：

​ $$ L_o{(p,w_o)} = \int_{\Theta(n)} f_t(p,w_o,w_i)L_i(p,w_i) cos(\theta_i) dw_i $$

上面的只局限在透射方向，就是法线方向的下半球。

BSSRDF

很多材质还会表现出下表面的光线传输。双向散射表面反射分布函数（BSSRDF）。

与反射分布函数和透射分布函数不同的是：散射的能量还需要考虑从其他附近入射点传递来的能量。

此时， 只考虑了当前点的入射，还需要考虑附近点的积累。

也就是说，在附近某一点$ p_i $ 处入射的能量与他最终离开$ p_o $点时能量的比例就是。

所以这个时候的积分需要考虑的不再是一个点，还需要考虑一片区域：

​ $$ L_o{(p_o,w_o)} = \int_A \int_{\Theta(n)} S(p_o,w_o,p_i,w_i) L_i(p_i,w_i) cos(\theta_i) dw_i dA $$

这个公式有如下特点：

辐射度理论

为什么将辐射度理论，就是为了更好的理解光线的发射与吸收的多少。

辐射通量（，也叫作功率）：单位时间内，穿过某一表面或空间的全部能量。

辐射度（）：表示穿过某一表面的通量面密度（可以理解成穿过单位面积的光线数量，可以理解亮度、光照强度）。

一个点光源发射光线，在具体他为r的位置，出辐射度为：

所以光照强度（就是单位面积光线数量，也就是通量面密度）按照距离的平方进行衰减的。

Lambertian定理

入射辐射度

Lambertian定理：到达表面的光线数量正比与光线方向和法线方向夹角的余弦。

如下图，一个面光源以$\theta$角度照射表面，面光源面积为$ A $,辐射通量为$ \Phi $，对应接受光照的表面面积为$ A1 $。如果A足够的小（这一点非常重要），那么对于A1内的点，入辐射度约为 。

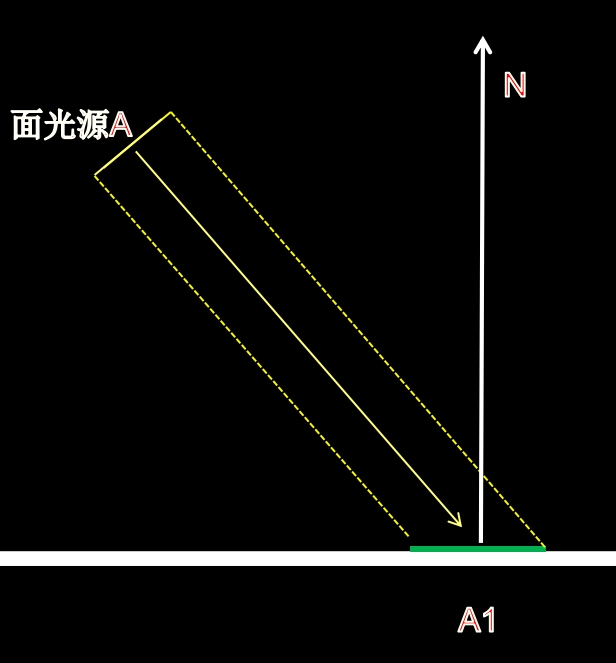
brdf_inlight

出射辐射度

Lambertian反射：反射方向的单位辐射度均匀分布=

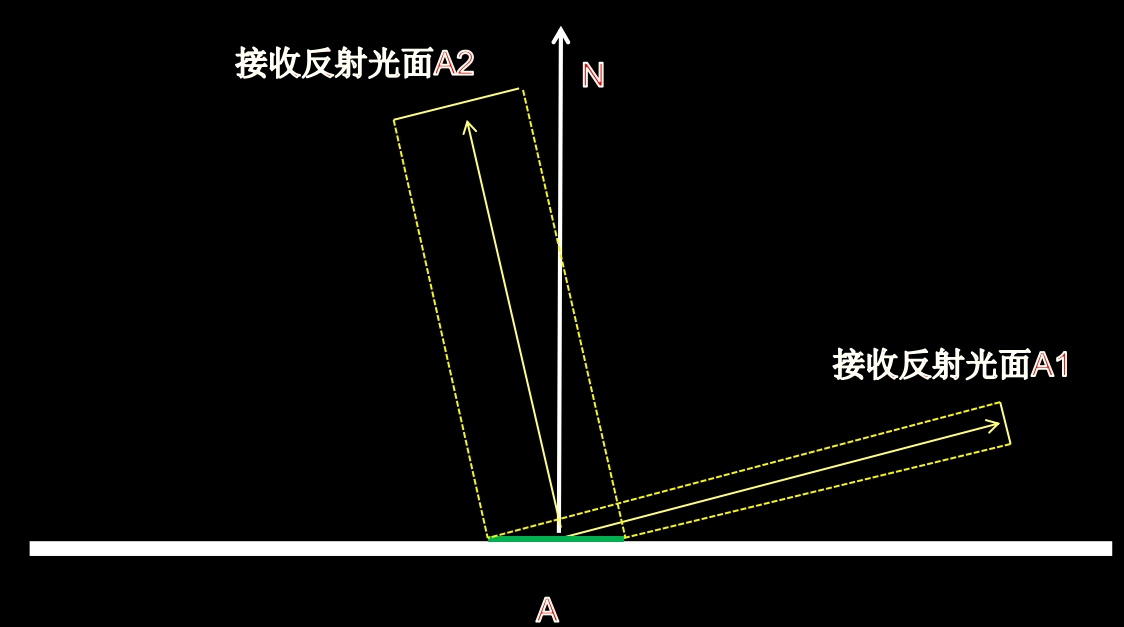
如下图，假如A处的光线是按照各个方向平均反射的，那么A1和A2接收到的光线总数是一样多的。但是，由于A1和A2的面积不一样，所以他们的辐射度（光照强度，亮度）是不一样的！！！

而Lambertian反射要求的是辐射度一样，所以光线的反射数量与反射方向和法线方向夹角的余弦成正比。

brdf_outlight

表面反射函数实践

首先BDRF的积分可以简化为求和，因为游戏引擎中光照都是通过有限个光源计算的，不在需要微分方向视椎体：

变成：

:为某个入射光方向。

: 一般就是经过距离衰减和阴影遮挡计算之后的光亮度。

: 就是

另一点需要注意的是，RGB通道的每个分量的颜色都是独立计算的。

下面我们将讨论具体的都是怎么计算的。

Lambertian反射

Lambertian模型可以作为最简单的BRDF模型，他是能量守恒的。

:表示的是表面反射率（Albedo\Diffuse），在实际中就是RGB通道的颜色值。

Lambertian为什么除$ \pi $

首先分析一种错误的理解：反射半球的表面积应该是，反射射光照总能量比例为，各个方向平均反射，所以最终lambertian反射强度应该是:

这种理解错误的原因是：Lambertian考虑的是反射辐通量（光照强度）各个方向恒定，而不是反射总辐通量R被平均分。

那么这个是怎么来的？

对幅通量根据Lambertian定律（反射幅通量和$ cos(\theta) $成正比）进行半球积分得到表面接收的辐通量。

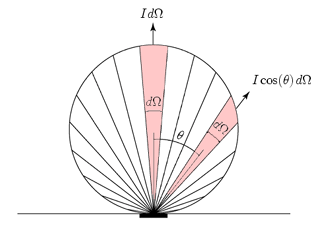
Lamberts-cosine-law

对所有方向的辐通量进行积分就可以得到反射全部的总辐射度：

有一个需要理解的地方：因某个方向的出辐射度为X（面积小），那么对其贡献辐射度的表面上的辐射度为$Xcos\theta$（面积大所以贡献的辐射度少）。

因为，Lambertian的brdf( )是常数：

进行移项：

下面对：反射半球半球积分 进行拆解和仔细计算：

所以：

假设入射辐通量为1，表面反射率为R（入射光被反射的比例），则反射辐通量（反射之后分布到各个方向后的比例）为：

至此，推导完毕。

菲涅尔方程

菲涅尔等式主要用来求解反射和透射系数。

首先需要，两种材质的折射率和 ,一般情况下随着光的波长折射率会有变化。

菲涅尔定律：

反射定律：

Unity Fresnel

real3 F_Schlick(real3 f0, real f90, real u)
{
    real x = 1.0 - u;
    real x2 = x * x;
    real x5 = x * x2 * x2;
    return f0 * (1.0 - x5) + (f90 * x5);        // sub mul mul mul sub mul mad*3
}

微表面模型 TODO

整体BRDF模型：

下面描述整体推到过程:

通量$ \Phi $

第一个概念是通量，单位时间穿过一个表面上光线的总量。（也就是功率）。

入射辐射度$ L_i $和反射辐射度$ L_o $

表示单位时间单位面积入射（反射）表面接受（反射）的光线量。

如果入射表面面积为， 则：

写成微分形式：

立体角$ w $和光强

光线传过单位立体角的数量。就是光强。微分形式：

辐射度$ L $

单位时间内传过单位立体角单位面积的光线量。

菲涅尔公式F

表示某一角度下光线被反射、折射的比例。 为入射通量，反射通量。则：

BDRF公式

​

这里的$ L_o $ 没有积分符号，是因为我们现在计算的是某一条线如何光线与某一条反射光线。

BDRF推导

在微面元理论中，我们的$ dA $由很多微面元组成，并且这些面元只有全镜面反射，只有满足的表面才能被反射出去。我们用统计模型来描述某个角度的面片比例。 那么入射的辐通量就需要考虑面片分布。则：

半角向量和出射角向量微分的对应关系:

1. 菲涅尔公式+BRDF公式：

2. 半角向量和出射角向量微分的对应关系:

3. 通过移项、约分构造brdf

4.除了上面的F、D之外，由于几何结构，还有一些光线由于几何结构被：masking 和 shadowing。所以这个比例为G项。

5.所以最终结果为：

法线分布函数：normal distribution function

D项：法线分布函数用来描述，法线方向在表面上的分布情况，积分结果为1。

几何衰减：Evaluate shadowing/masking term

G项：用来描述Shadow和masking项。用来描述不同的几何结构有多少光线被遮挡。

菲涅尔项：Fresnel

F项：用来描述在不同材质，不同角度上，反射光线所占的比例。

unity中的实现

Unity Specular Term

    case 0: specularTerm = ComputeWard(H, LdotH, NdotL, NdotV, positionWS, preLightData, bsdfData); break;
    case 1: specularTerm = ComputeBlinnPhong(H, LdotH, NdotL, NdotV, positionWS, preLightData, bsdfData); break;
    case 2: specularTerm = ComputeCookTorrance(H, LdotH, NdotL, NdotV, positionWS, preLightData, bsdfData); break;
    case 3: specularTerm = ComputeGGX(H, LdotH, NdotL, NdotV, positionWS, preLightData, bsdfData); break;
    case 4: specularTerm = ComputePhong(H, LdotH, NdotL, NdotV, positionWS, preLightData, bsdfData); break;

Unity Specular Term

Lambert
OrenNayar