- IBL理论与应用
- 理论基础
- 光照函数
- 代码
- IBL优化:Split Sum Approximation
- IBL光照函数积分估计
- 原始积分
- 拟合积分优化
- 预积分贴图
IBL理论与应用
这部分内容主要参自UE4的论文[Real Shading in Unreal Engine 4]
IBL主要指的就是环境贴图部分计算的光照。
理论基础
光照函数
光源就是一个Cubemap,过去也会用到双剖面。实际的积分光照结果是:
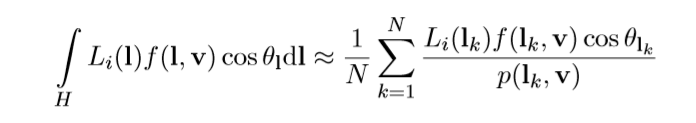
代码
这部分内容对应的代码就是下面的:
// 根据一个随机Xi值和粗糙度、法线计算需要采样cubemap的方向,
float3 ImportanceSampleGGX( float2 Xi, float Roughness, float3 N ) {
float a = Roughness * Roughness;
float Phi = 2 * PI * Xi.x;
float CosTheta = sqrt( (1 - Xi.y) / ( 1 + (a*a - 1) * Xi.y ) );
float SinTheta = sqrt( 1 - CosTheta * CosTheta );
float3 H;
H.x = SinTheta * cos( Phi );
H.y = SinTheta * sin( Phi );
H.z = CosTheta;
float3 UpVector = abs(N.z) < 0.999 ? float3(0,0,1) : float3(1,0,0);
float3 TangentX = normalize( cross( UpVector, N ) );
float3 TangentY = cross( N, TangentX ); // Tangent to world space
return TangentX * H.x + TangentY * H.y + N * H.z;
}
//N就是NumSamples,是进行采样估计得采样数,决定了积分准确度,可以看到和正常光照一样需要有FDG的计算
float3 SpecularIBL( float3 SpecularColor, float Roughness, float3 N, float3 V )
{
float3 SpecularLighting = 0;
const uint NumSamples = 1024;
for( uint i = 0; i < NumSamples; i++ )
{
float2 Xi = Hammersley( i, NumSamples );
float3 H = ImportanceSampleGGX( Xi, Roughness, N );
float3 L = 2 * dot( V, H ) * H - V;
float NoV = saturate( dot( N, V ) );
float NoL = saturate( dot( N, L ) );
float NoH = saturate( dot( N, H ) );
float VoH = saturate( dot( V, H ) );
if( NoL > 0 )
{
float3 SampleColor = EnvMap.SampleLevel( EnvMapSampler, L, 0 ).rgb;
float G = G_Smith( Roughness, NoV, NoL );
float Fc = pow( 1 - VoH, 5 );
float3 F = (1 - Fc) * SpecularColor + Fc;
// Incident light = SampleColor * NoL
// Microfacet specular = D*G*F / (4*NoL*NoV)
// pdf = D * NoH / (4 * VoH)
SpecularLighting += SampleColor * F * G * VoH / (NoH * NoV);
}
}
return SpecularLighting / NumSamples;
}
IBL优化:Split Sum Approximation
由于上面内容如果实时计算的话,开销太高,所以对原始公式进行了一次估计。变成了:
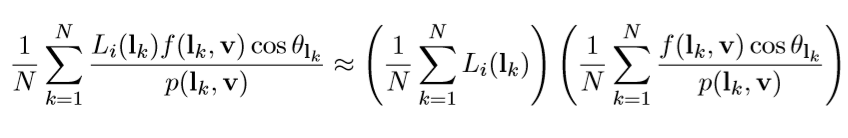
这个就叫做Split Sum Approximation。
优化之后的代码:
float3 ApproximateSpecularIBL( float3 SpecularColor, float Roughness, float3 N, float3 V )
{
float NoV = saturate( dot( N, V ) );
float3 R = 2 * dot( V, N ) * N - V;
// 第一项的优化结果:mipmap某一层
float3 PrefilteredColor = PrefilterEnvMap( Roughness, R );
// 第二项优化结果:真实的进行采样积分,或者使用估计值。
float2 EnvBRDF = IntegrateBRDF( Roughness, NoV );
return PrefilteredColor * ( SpecularColor * EnvBRDF.x + EnvBRDF.y );
}
得到上面的公式之后进行两个积分项的分别化简。
IBL MipMap构造与Prefilter
首先是第一项,实际上就是计算一个颜色的平均值。
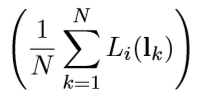
根据不同的粗糙度采样的范围有所区别。粗糙度越大,采样越分散,所以通常就使用了mipmap对应于不同的粗糙度(也就是模糊程度不同的平均值)。根据其他的一些数学推导,模糊用的filter有所区别。
UE4进行Prefilter的代码:
float3 PrefilterEnvMap( float Roughness, float3 R )
{
float3 N = R; float3 V = R;
float3 PrefilteredColor = 0;
const uint NumSamples = 1024;
for( uint i = 0; i < NumSamples; i++ )
{
float2 Xi = Hammersley( i, NumSamples );
float3 H = ImportanceSampleGGX( Xi, Roughness, N );
float3 L = 2 * dot( V, H ) * H - V;
float NoL = saturate( dot( N, L ) );
if( NoL > 0 )
{
PrefilteredColor += EnvMap.SampleLevel( EnvMapSampler, L, 0 ).rgb * NoL;
TotalWeight += NoL;
}
}
return PrefilteredColor / TotalWeight;
}
IBL光照函数积分估计
然后是第二项:
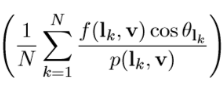
这一项的优化方式是:
- 先得到一个真实的曲线。然后创造一个函数去拟合这个积分结果。
- 或者不拟合直接用原始积分结果。
- 把准确的积分结果保存在贴图中:UE4的做法
原始积分
真实的积分代码:
// 真实的积分代码:
float2 IntegrateBRDF( float Roughness, float NoV )
{
float3 V; V.x = sqrt( 1.0f - NoV * NoV ); // sin V.y = 0; V.z = NoV; // cos
float A = 0;
float B = 0;
const uint NumSamples = 1024;
for( uint i = 0; i < NumSamples; i++ )
{
float2 Xi = Hammersley( i, NumSamples );
float3 H = ImportanceSampleGGX( Xi, Roughness, N );
float3 L = 2 * dot( V, H ) * H - V;
float NoL = saturate( L.z ); float NoH = saturate( H.z );
float VoH = saturate( dot( V, H ) );
if( NoL > 0 )
{
float G = G_Smith( Roughness, NoV, NoL );
float G_Vis = G * VoH / (NoH * NoV);
float Fc = pow( 1 - VoH, 5 );
A += (1 - Fc) * G_Vis;
B += Fc * G_Vis;
}
}
return float2( A, B ) / NumSamples;
}
拟合积分优化
拟合的方式可以参考文献:
[Summary of Physically Based Shading in Call of Duty: Black Ops ]
文献当中提到了真实曲线和如何构造出估计曲线。
估计拟合的brdf代码:
float3 EnvironmentBRDF( float g, float NoV, float3 rf0 )
{
float4 t = float4( 1/0.96, 0.475, (0.0275 - 0.25 * 0.04)/0.96, 0.25 );
t *= float4( g, g, g, g );
t += float4( 0, 0, (0.015 - 0.75 * 0.04)/0.96, 0.75 );
float a0 = t.x * min( t.y, exp2( -9.28 * NoV ) ) + t.z;
float a1 = t.w;
return saturate( a0 + rf0 * ( a1 - a0 ) );
}
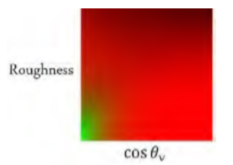
预积分贴图
UE4Brdf的积分贴图: