- 浮点数的作用
- 浮点数回顾
- 标准和低精度浮点数
- 浮点数范围解释
- 低精度尾数位问题举例
- 低精度尾数位问题可视化展示
- 低精度不均匀尾数位长度问题
- 颜色缩放失效
GPU浮点数的精确度以及注意事项
在hdr的开发流程中,pbr的灯光计算结果和特效的亮度理论上是没有上限,但是需要保存到Color Buffer当中,这就涉及到Color Buffer的数据精度,通常Color Buffer的格式是R11G11B10F。所以需要进行Min操作,来保证保存到RT当中的数据没有溢出,因为计算的精度通常是half或者float要比保存的精确度高。所以会有一些问题,下面找到了资料来讨论Float精确度相关的问题。
内容主要摘录一部分自:参考链接,并作了补充和例子说明,本文主要为了说明Color Buffer浮点数范围问题,原文对误差部分做了更详细的讨论。
浮点数的作用
通常颜色在渲染中的表示不是整型,而是浮点数。浮点数有很大的浮动范围可以用于:
- 编码HDR的颜色和记录光照。
- 当操作多个颜色的混合滤波需要分数。
- 在黑暗区域不通过Gamma编码也可以表示更大的精确度。
- 需要量化边界相对误差
- 浮点数是GPU的自然表示(GPU很长一段时间没有整数的支持,并且用浮点数模拟,并且现在整数的操作比浮点数慢)。
即便浮点数十分重要,但是我们很少存储32bit的浮点数值,即便是HDR的颜色。因为内存带宽和性能两部分的限制。内存带宽和缓存通常是重要的资源,最基础的经验法则是: “ALU is cheap, memory access is expensive”。即便是最简单的内存访问操作也需要上百个时钟周期的延迟。并且纹理单元的开销更高,应为需要滤波等开销很高的操作。
因此,渲染程序员通常使用低精度的浮点数格式来保存浮点数。两个最常用的是RGBA16F(4通道的16bit的单精度浮点数)和R11G11B10F(R和G通道使用11bit,B通道使用10bit)。
下面先分析IEEE的32bit浮点数和上述浮点数格式的区别:
浮点数回顾
浮点数的表示方式:
-
符号位sign:一个bit用来表示符号位。在数据最前面的一个bit,可选。
-
指数位exponent:多个Bit用来表示2的指数幂和剩余的数相乘,阶码是有偏移的,单精度偏移是127(0000001 表示 -126 11111110 表示127 而全0和全1有特殊用处),双精度是1024。 11bit和10bit 指数位5位偏移应该是15
-
尾数位mantissa:多个bit用来表示数据的表示小数部分,和指数位结果相乘,通常假设小数点前整数位是1(这个是IEEE 754标准,其他标准也可能会约定小点后第一位始终是1)。例如:如果尾数位是01011000 ,那么他表示的数是:1.01011000
所以最终表示是数是:
参见对指数位的说明,对很多特殊的编码,指数位使用了特殊的值。这里只讨论一个:0的编码,通过将指数和尾数都设置成0,由于符号位可以设置,所以会存在两个0 (+0 和-0)。
浮点数是一种非常聪明的表示法,它具有许多很好的属性(例如,正浮点数可以解释为整数可以直观的排序或计算最小/最大,并且整数0对应于正的浮点数0)。然而,伴随而来的是许多精度问题,这些问题并不总是最直观的。下面来谈论这些问题。
标准和低精度浮点数
下面是常用的浮点数格式和编码方式。
| Bit depth | Sign bit present? | Exponent bits | Mantissa bits |
|---|---|---|---|
| 32 | Yes | 8 | 23 |
| 16 | Yes | 5 | 10 |
| 11 | No | 5 | 6 |
| 10 | No | 5 | 5 |
可以发现一些规律:
- 11和10位的浮点数没有符号位,主要是由于本身精确度并不高,并且通常被图形API用作保存颜色的格式,所以没有必要使用符号位。
- 16bit的half类型和11bit、10bit有相同的指数位。但是有符号位,整数和负数有相同的范围。5位的指数位可以保证最大到64500到65500之间(见下方解释)
浮点数范围解释
这里主要讨论16bit、11bit和10bit的浮点数上限,因为32bit的浮点数完成光照计算之后要进行Min操作,然后才能保存到RT当中,所以Min的操作数十分关键。
由于这三个类型的指数位都相同,所以上限依赖于尾数位的数量:
-
16位的float,尾数最大可以表示1.1111111111 ,十进制为1.9990234375;5位指数位,计算偏移15,那么最大可以表示11110 =15,指数部分就是32768,最大的数就是32768*1.9990234375,约为65,504。
-
11bit的浮点数,尾数最大可以表示1.111111,十进制为1.984375;5位指数位,计算偏移15,那么最大可以表示11110 =15,指数部分就是32768,最大数就是32768*1.984375= 65,024 。
-
10bit的浮点数,尾数最大可以表示1.11111,十进制为1.96875;5位指数位,计算偏移15,那么最大可以表示11110 =15,指数部分就是32768,最大为32768*1.96875=64,512)
综上所述在保存数据的时候如果不清楚引擎当中如何设置hdr Color buffer类型,Min的上限设置成64500是最安全的。
低精度尾数位问题举例
首先看一个用8位整数表示0-1的例子:
N[252/255, 8] = 0.98823529
N[253/255, 8] = 0.99215686
N[254/255, 8] = 0.99607843
接下来用二进制小数表示他们:
BaseForm[N[2*252/255, 8], 2] = 1.1111100111111001111110100
BaseForm[N[2*253/255, 8], 2] = 1.1111101111111011111111000
BaseForm[N[2*254/255, 8], 2] = 1.1111110111111101111111100
我高亮了前五位小数位。我们知道10bit的浮点数只有5bit的尾数位,可以发现10bit的浮点数甚至不能精确地表示8bit整型颜色(因为5bit尾数不足以区分这三个颜色,主要原因有效位太短)。于此同时,你能够看到下一位是不同的,因此在11bit的浮点数中可以被区分出来,这就会造成白色的错误表示。
低精度尾数位问题可视化展示
好的,我们知道低位数的浮点数甚至不能准确地表示简单的8位亮度。但是会差到什么程度呢?
我们创建了尾数位的可视化效果。

随着数值增大误差也快速增加。
我们通常不使用8bit的线性值保存颜色, 因为为了节省精度,保存人眼更敏感的部分(暗部),所以用Gamma。下面是考虑了Gamma编码的误差结果。
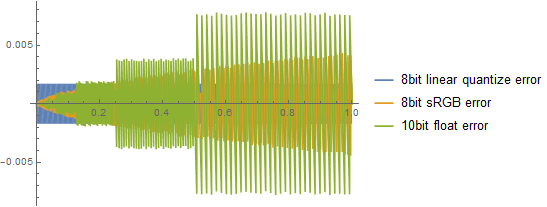
这部分主要展示了不同的数据有效位对于颜色误差的影响。为什么随着数据变大误差会变大?因为数据越大需要的有效位数越多,但是可用的有效位又是固定的,所以会呈现上面的效果。
低精度不均匀尾数位长度问题
由于R11G11B10类型的浮点数有不均的尾数,我们量化他们的区别。
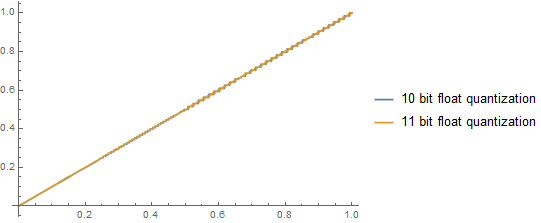
数值越大误差越大。
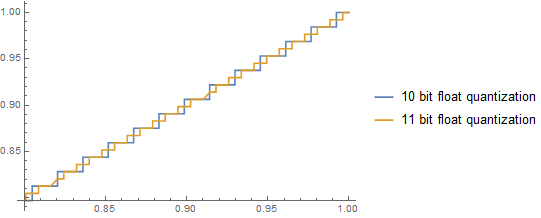
这种误差意味着什么?下面是从0.5到0.6的颜色变化,产生了错误的饱和度。

如何显示器好,这个效果会更加明显,例如hdr显示器有更加精确的显示范围和色域,可以看到:
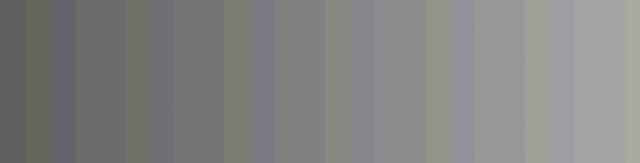
可以通过改变颜色动态范围和dithering来修正这样的效果。
颜色缩放失效
有一个常见的错误关键,乘上一个大数就可以对浮点数进行编码提升精确度,然后解码。这是无效的。下面是量化数据:
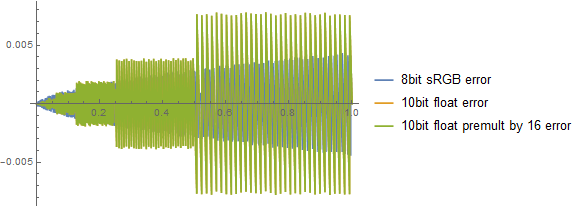
可以看到没有区别,这是因为有效位数没有变化,所以表示的精度也没有变化。也就是说尾数位没有变化,变化的只有指数位。
我们可以设置不同的缩放值看看误差,误差也只是左右移动了:
